本文简要总结了笔者对视频编码技术中码率控制算法的理解。例子的范围限制在从H.264至今的编码标准，更早的编码标准笔者并没有了解过。
名词解释
- 视频编码（video encoding）：将视频的原始像素数据压缩为符合某些标准（比如H.264）的二进制数据的过程。
- 码率（bitrate）：单位时间内的数据量，一般用bps（bits per second）作为单位。
- MB：宏块（macro block），实际上在不同的编码标准中它有不同的叫法，但本文使用H.264/AVC中的MB。它是视频编码的基本单元，常见的大小有16x16、64x64等。编码时每一帧画面都会被按照固定大小分割成大量MB，再一个个处理。
- QP：量化参数（quantization parameter）。视频压缩一般为有损压缩，编码时需要为每一帧以及每一个MB选择QP，用以控制画面质量与码率。QP越大，则损失的信息越多，画面质量越差，但压缩率也越高。
- Q step：量化步长（quantization step）。上面提到的QP实际仅是个序号，在熵编码时使用。真正用来对数据做量化的其实是量化步长。它是一组浮点数，与QP一一对应。如果你不清楚什么是量化，可以通俗地理解为一种调整数据精度的操作。比如测量物体重量，精度要求高时用克，精度要求低时用吨。
码控的类型
视频编码的码率控制（Rate-Control），主要指编码过程中，通过调整QP来控制视频码率的行为。在不同的使用场景下，用户对视频的码率大小、稳定性会有不同的要求，因此码率控制的类型也多种多样。
比如观看离线视频文件时，往往不需要此视频具备恒定的码率。因为整个文件都在本地，只要磁盘IO和设备解码能力都合格，基本就不会发生卡顿问题（这里不讨论硬件解码的buffer限制以及内网带宽限制）。所以压制这类视频时会倾向于在相同的文件大小下保证画面质量而非码率平稳性。画面纹理比较复杂或运动剧烈的场景，码率给高一些，以保证画面质量；而画面简单的场景，码率就给低一些，节省硬盘空间。这种码控策略我们统称为可变码率（VBR）。
但在观看在线视频时，由于用户带宽有限，客户端缓存的数据量也有限，所以需要对码率做一些限制。否则一些瞬时码率过高的片段可能会引起卡顿。此外还有一点，由于CDN是按流量计费的，视频网站如果使用VBR编码视频会使带宽成本变得不可控。所以压制这类视频时，会倾向于选择恒定码率（CBR）。
不同场景下的码控需求（相同文件大小的前提下）
本文接下来的讨论内容主要集中在CBR，但其中的一些改良算法其实也可以用在VBR。
码控的根基：RQ模型
首先看一下码率控制的大体流程：
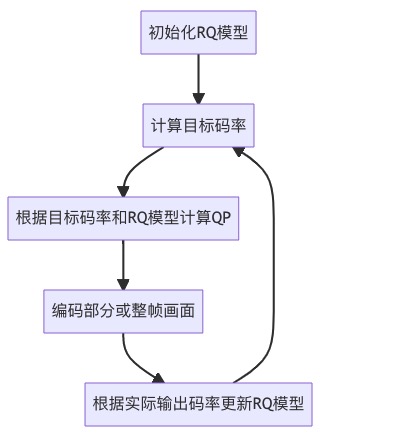码控基本流程
可以看到整个流程都是围绕着RQ模型进行。这里的RQ模型指的是码率（Rate）与量化参数（QP）的推导关系，可以说是码控算法的根基。它经历过多次改进，精度也在不断提高，这里举几个例子：
- 一阶模型：
最简单的模型，在x264、OpenH264等编码器中被广泛使用。式中Comp表示图像复杂度，一般可以使用MAD（Mean Absolute Difference）来计算。α是一个系数，需要我们在编码过程中不断根据实际输出码率来更新。
- 二阶模型：
一阶模型的进阶版，JM中有使用。
- R-λ模型：
在HM（HEVC Test Model）中被引入的模型[1]，显著提升了码控精度。式中的λ是率失真优化中使用的拉格朗日乘子，放在下节作为拓展内容介绍。而f(λ)则是通过实验拟合得到的。比如HM中就是：
\[QP = 4.2005lnλ+13.7112 \tag{4}\]MAD值的获取与模型的更新
上面提到RQ模型中使用的图像复杂度可以使用MAD来计算。但是当前帧的MAD值只能在编码后才能得到，因为MAD的计算需要用到编码产生的数据，这与QP需要在编码前确定这一点相矛盾。另外，在模型确定后，我们还需要确定模型的更新方式及速率。通过提高模型系数的更新速率，可以使编码器的输出码率更加平稳；但相对的，画面质量可能由于QP变化幅度过大而下降。
针对这些问题，不同的编码器选择了不同的方案：
- 在JM中，使用了一个一阶线性模型根据过去帧的MAD来预测当前帧的对应值。而RQ模型的系数α则直接通过当前帧的编码结果来反向计算得到。
- 在OpenH264和x264中，则放弃了MAD的计算，转而合并了$α \cdot Comp$，把它作为一个整体，用编码结果来更新。
- 对于R-λ模型，其提出者也已经设计了对应的更新公式和经验值供我们参考[1]。
模型更新这部分内容，更多是工程实践上的考量，需要根据经验和测试情况不断调整。
拓展：λ是什么
R-λ模型中的λ是率失真优化（Rate-distortion optimization，RDO）中的一个系数。这里的率失真优化，指的是编码过程中的一个优化步骤。要详细解释它，我们需要先了解率失真理论。它起源于香农的研究[2]，大致可以概括为：在给定的信源分布以及可接受的失真度D下，求信息数据量R的理论最小值。显然，可接受的D越大，其对应的R也就越小。这个R-D的关系边界，我们称为率失真曲线，即下图中的红线[3]。旁边的绿线则是编码器实际工作区域的边界，它和理论值存在一定差距。
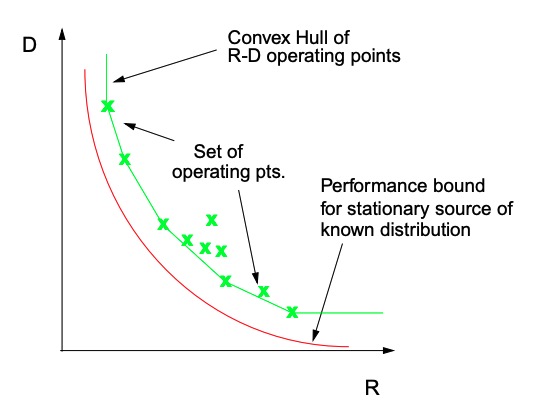R-D曲线
视频编码标准提供了大量的工具集，或者说编码模式，它们就相当于上图的绿点，使用它们会产生不同大小的失真和压缩率。在它们之中选择一个恰当的来使用是一件比较复杂的事情。注意到这个问题本质是一个数学最优化问题，所以可以利用拉格朗日乘数法的离散形式来解决它。简单地说，引入一个拉格朗日乘子λ，构建代价函数，再去求取代价函数的最小值即可：
\[\begin{cases} min\{J\} \\ J(λ)=D+λ \cdot R \end{cases}\tag{5}\]通俗地理解，λ就相当于失真与码率的权值。给定了λ，也就给定了一个判定模式好坏的标准。如下图所示，求代价函数最小值，相当于求斜率为λ的直线与R-D曲线的切点。在编码过程中，不论是模式选择，还是运动矢量的比较，都会利用到这个方法。
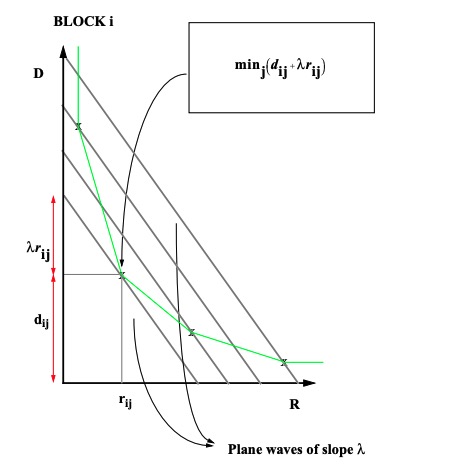拉格朗日乘子与R-D曲线斜率
R-λ模型的提出者首先根据实验数据提出R-D曲线可以近似拟合为一条双曲线，再根据λ是R-D曲线斜率这一点，求得了R-λ模型：
\[\begin{cases} D(R)=CR^{-K} \\ λ=-\frac{∂D}{∂R}=CKR^{-K-1}=α' \cdot R^{β'}\end{cases}\tag{6}\]码控优化算法
上文介绍的内容，属于码控核心算法，其目的仅为控制输出码率，使其尽可能地接近目标。但在实际应用中，我们并不需要这么严格地执行。在输出码率基本满足要求的前提下，我们依然有一定的调整空间来改善画面质量。下文将介绍几种这方面的算法。
Adaptive-Quantization
由于人眼对不同类型的画面的细节感知程度是不同的，所以给不同画面内容给予相同的权重来分配码率实际上是比较浪费的。比如高速运动的物体就可以相对静态物体模糊一点。在这方面做文章的算法一般归类为基于感知的码控算法。而其中一类比较简单且使用广泛的算法，叫做Adaptive Quantization（AQ）。简单来说，它利用图像的方差或其他类似特征来衡量当前宏块的复杂度，对于内容较复杂的宏块，算法认为可以适当舍弃其细节，所以增大其QP；而简单的宏块则反之。经过这种调整，视频的主观质量能得到大幅提升。如今很多编码器都实现了AQ，比如x264的实现如下所示。计算得到的qp_adj即QP偏移量，会叠加到R-Q模型计算出来的QP上：
1
2
3
// x264的AQ核心实现。ac_energy_mb计算宏块像素值方差。strength代表AQ强度，由用户配置。
uint32_t energy = ac_energy_mb( h, mb_x, mb_y, frame );
qp_adj = strength * (x264_log2( X264_MAX(energy, 1) ) - (14.427f + 2*(BIT_DEPTH-8)));
利用人眼感知能力的码控算法还有很多，比如基于最小可觉察误差(JND, Just Noticeable Distortion)的，或者基于机器学习的，这里不再展开。值得一提的是，由于是针对主观视觉体验的优化算法，通过PSNR等客观手段测试往往无法体现这些算法的优势。
MB-Tree
MB-Tree是由x264的开发者提出的算法，它的基本思想是：由于视频数据在编码时存在依赖关系，被参考的数据的失真程度直接影响到后续的预测精度，所以根据依赖关系给予不同画面不同码率权重可以从整体上提升画面质量。
MB-Tree的实现依赖于x264内部的lookahead结构。所谓的lookahead，是一种预编码模块。它会使用经过下采样的低分辨率图像预先对视频进行一轮编码（这种预编码只进行到SATD的计算），并缓存大量有用的信息供后续正式编码使用。我们在使用x264编码视频时，经常会看到-lookahead参数，它表示预编码的帧数，增加这个值利于提升编码质量，但是会增加编码时延。
有了lookahead缓存下来的信息，我们就可以从最后一帧开始，逐帧回溯每个MB的依赖性，或者说重要性，再根据这个重要性计算QP的偏移量。MB-Tree的原理非常有特色，如果读者对细节感兴趣，推荐阅读x264开发者的文章[4]。
总结
本文仅概述了一些码控算法的基本思想和原理，想要深入理解这些算法，还是需要阅读论文和源码。笔者看过的代码中，JM和OpenH264的码控算法属于比较容易阅读的（起码比x264容易懂），推荐感兴趣的读者从这两个开始。
参考文献
[1] JCTVC-K0103
[2] C.E. Shannon. Coding theorems for a discrete source with a fidelity criterion. In IRENational Conventwn Record, Part4, pp. 142-163, 1959.
[3] A. Ortega; K. Ramchandran. Rate-distortion methods for image and video compression. IEEE Signal Processing Magazine, Volume: 15, Issue: 6, Nov 1998.
[4] Garrett-Glaser J. A novel macroblock-tree algorithm for high-performance optimization of dependent video coding in H.264/AVC[J]. Tech. Rep., 2009.