本文以WebRTC中的FrameBuffer为例，介绍了基于卡尔曼滤波的Jitter Buffer的原理。
前言
由于网络带宽以及视频码率都不是恒定的，当视频数据在网络传输时，各帧数据实际上并不是按照帧率匀速到达的，即存在抖动（Jitter）。为了保证在线播放视频时帧率稳定，不出现快慢放，客户端往往会在本地缓存一段数据，再按照帧率读取渲染。这个机制我们可以称之为Jitter Buffer。显然的，允许缓存的数据越多，视频卡顿的概率越低。在点播场景下，我们可以简单地设置一个较大的Buffer来换取播放的流畅性。但对于实时音视频通话等时延敏感应用来说，增大缓存意味着增加时延，会极大地降低用户体验。所以如何决策出合适的Buffer大小就成为了一个需要优化的内容。注意本文中衡量Jitter Buffer大小的单位都使用时间，而非字节数，这样便于表达。
Jitter Buffer多大最合适
笔者在思考这个问题时，第一个想法是，直接统计传输耗时最长的那一帧，计算让它不卡顿需要预留多长时间，就可以作为Jitter Buffer的大小了。但是很显然WebRTC并没有这么做，不然也就不会有本文了。原因可能是样本的噪声以及复杂多变的网络环境让这种统计结果变得不够可靠与实时，导致效果欠佳。
那么为了设计更好的方案，首先整理一下Jitter的原理。这里将Jitter的产生原因归一下类：
- 视频的关键帧机制以及码率本身的不稳定导致每帧的大小不同，所以各帧需要不同的传输时间
- 网络本身的变化，链路切换、拥塞、噪声等
- 网络存在丢包，重传数据会增加rtt级别的时延
WebRTC中的Jitter Buffer基本仅考虑前两点。虽然在代码中能看到有尝试过针对丢包进行优化，但是实现方案很原始，默认并没有开启。笔者认为原因有以下几点：
- WebRTC的带宽估计算法是基于时延变化运作的，相比基于丢包的算法敏感度更高，产生拥塞丢包的可能性较低
- WebRTC有实现FEC（前向纠错），可以不依靠重传解决部分丢包场景
- 即便Jitter Buffer成功抗住了重传导致的抖动，其代价往往也是百毫秒以上的时延增加。对于RTC应用来说，是偶尔看到视频卡一下，还是全程顶着高时延通话，其实不太好说哪个更体验好
所以本文接下来也不考虑重传的影响。接下来，给出理论上各帧视频数据的传输时间：
\[T = T_{tunnel} + \frac{Size}{rate_{recv}} \tag{1}\]式中的$T_{tunnel}$指网络固有延迟，注意当对端发送码率大于网络实际承载能力时，随着阻塞在网络上的数据逐渐累积，该值亦会逐渐增涨。而$rate_{recv}$（接收速率）我们可以认为是对端发送码率和网络实际带宽的较小值。因为越大的帧传输越慢，所以理论上只要我们给最大的帧留够buffer，让它在传输完成时刚好赶上需要播放它的时间，就可以保证视频能够稳定匀速地播放了。因此，需要的buffer大小，或者说需要主动预留的延迟时间，可以大致按照下式计算：
\[Buffer = T_{max} - T_{avg} = \frac{Size_{max}-Size_{avg}}{rate_{recv}} \tag{2}\]式中的帧大小我们可以在接收端通过统计直接得到，而$rate_{recv}$则是一个需要跟踪的未知参数，接下来介绍其计算方法。
接收速率的计算
因为帧数据的实际发送不是连续的，而是按照采集帧率有一定间隔地发送。所以直接将帧大小除以两帧之间的时间间隔是不行的。这里我们只能通过计算不同帧的差值来计算接收码率：
\[rate_{recv} = \frac{Size_{delta}}{T_{delta}} \tag{3}\]式中的$T_{delta}$如下图中所示。
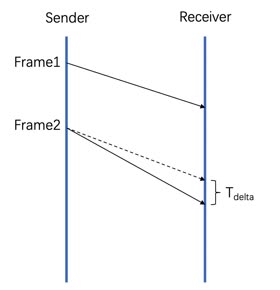Tdelta的获取
由于该值一般很小，它的测量精度和噪声导致我们没办法直接使用它计算。在工程应用中，我们一般使用各类滤波器（Filter）来处理这种情况。即对样本做加权处理，以得到比较稳定且准确的预测结果。最简单的例子就是求平均值。而当系统的状态会随时间变化时，我们也可以通过逐渐降低靠前的样本的权重来跟踪。但是简单的滤波器严重依赖权值的定义，跟踪的响应速度和准确性都十分有限，不能保证在所有网络环境下都好好工作。WebRTC在这里采用了有名的卡尔曼滤波[1]，其运算量低的同时效果也很优秀，并且能够同时输出参数的概率分布。不了解卡尔曼滤波但感兴趣的读者可以阅读此文章，讲得比较通俗易懂。本节接下来的内容需要一定卡尔曼滤波相关知识。不感兴趣的读者可以跳到下一节。
WebRTC对卡尔曼滤波的实现，集中在jitter_estimator.cc文件中，主要分为两个函数。一个用于更新模型，计算接收速率；一个用于更新样本与预测值的偏差，在最后计算结果时会使用。本文并不打算对着卡尔曼滤波公式一个一个讲解，这里先贴一下核心代码，后续补充解释：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
void VCMJitterEstimator::KalmanEstimateChannel(int64_t frameDelayMS,
int32_t deltaFSBytes) {
double Mh[2];
double hMh_sigma;
double kalmanGain[2];
double measureRes;
double t00, t01;
// Prediction
// M = M + Q
_thetaCov[0][0] += _Qcov[0][0];
_thetaCov[0][1] += _Qcov[0][1];
_thetaCov[1][0] += _Qcov[1][0];
_thetaCov[1][1] += _Qcov[1][1];
// Kalman gain
// K = M*h'/(sigma2n + h*M*h') = M*h'/(1 + h*M*h')
// h = [dFS 1]
// Mh = M*h'
// hMh_sigma = h*M*h' + R
Mh[0] = _thetaCov[0][0] * deltaFSBytes + _thetaCov[0][1];
Mh[1] = _thetaCov[1][0] * deltaFSBytes + _thetaCov[1][1];
// sigma weights measurements with a small deltaFS as noisy and
// measurements with large deltaFS as good
double sigma = (300.0 * exp(-fabs(static_cast<double>(deltaFSBytes)) / (1e0 * _maxFrameSize)) + 1) * sqrt(_varNoise);
hMh_sigma = deltaFSBytes * Mh[0] + Mh[1] + sigma;
kalmanGain[0] = Mh[0] / hMh_sigma;
kalmanGain[1] = Mh[1] / hMh_sigma;
// Correction
// theta = theta + K*(dT - h*theta)
measureRes = frameDelayMS - (deltaFSBytes * _theta[0] + _theta[1]);
_theta[0] += kalmanGain[0] * measureRes;
_theta[1] += kalmanGain[1] * measureRes;
// M = (I - K*h)*M
t00 = _thetaCov[0][0];
t01 = _thetaCov[0][1];
_thetaCov[0][0] = (1 - kalmanGain[0] * deltaFSBytes) * t00 -
kalmanGain[0] * _thetaCov[1][0];
_thetaCov[0][1] = (1 - kalmanGain[0] * deltaFSBytes) * t01 -
kalmanGain[0] * _thetaCov[1][1];
_thetaCov[1][0] = _thetaCov[1][0] * (1 - kalmanGain[1]) -
kalmanGain[1] * deltaFSBytes * t00;
_thetaCov[1][1] = _thetaCov[1][1] * (1 - kalmanGain[1]) -
kalmanGain[1] * deltaFSBytes * t01;
}
其实注释已经解释了大部分内容，这段代码将测量样本带入卡尔曼滤波的迭代公式来更新模型。其状态外推方程（State Extrapolation）和协方差外推方程（Covariance Extrapolation）都设定为了不变（乘以单位矩阵）。系统状态参数是_theta[0]和_theta[1]，其观察方程即代码deltaFSBytes * _theta[0] + _theta[1]。可以按下式理解：
_theta[0]就是$Rate_{recv}$的倒数，上文解释过，这是我们的目标值。而_theta[1]（$T_{offset}$），就是一个和帧大小无关的偏移量。当网络处于逐渐拥塞的状态时，其值为正，当网络从拥塞中恢复时，其值为负。另外，代码中的sigma变量即测量不确定度（Measurement Uncertainty），就像注释里说的，因为deltaFSBytes越大，时间差越大，样本精度就越高，所以根据其大小给予不同权重。
目标Buffer的计算
每收到一帧，我们都得到一个测量样本（frameDelayMS和deltaFSBytes），通过不断迭代更新模型，即可获取到接受速率。似乎接下来就可以直接根据公式(2)来计算Jitter Buffer的大小了。但是这还不够，因为这是个有噪声的系统，而前面计算出的仅仅是期望值。如果直接使用这个值作为buffer，即便预测值是准确的，系统在接收到最大帧时仍然有50%的几率卡顿。这里我们还应该考虑噪声的分布。这也是WebRTC采用卡尔曼滤波的原因之一。
这部分内容较为简单，即高中学习的正态分布置信区间的应用。每次拿到样本时，除了更新卡尔曼滤波模型，还要统计模型预测结果和实际测量值的偏差（即统计样本和公式(4)的差值），计算其方差$σ^2$。然后就可以得到在期望值上需要增加的偏移量了：
\[T_{offset} = 2.33 * σ - 30ms \tag{5}\]式中的常量都是WebRTC定义的经验值。2.33是正态分布表（z-table）中99.01%的那一项，整个式子表示算法可以接受有1%的概率出现超过30毫秒的卡顿。最后，再加上公式（2），我们就得到了Jitter Buffer的最终输出：
遗留问题及总结
本文介绍了Jitter Buffer的核心逻辑。但是遗留了两个问题笔者还没有想清楚。一个是卡尔曼滤波的观察方程建模包含了一个偏移量（_theta[1]），但计算Jitter Buffer时却并没有使用它。虽然感觉可以接受，毕竟只有网络拥塞时这个值才有意义，但还是缺乏一个完整的解释。还有一个问题是卡尔曼滤波本身已经统计了系统状态的概率分布了（即协方差矩阵_thetaCov），直接使用它应该也可以得到类似式（5）中的$T_{offset}$。但是WebRTC额外进行了统计，原因是什么呢。如果读者有答案，欢迎讨论。
另外，在实际应用Jitter Buffer时，还涉及到等待队列控制，各种时间戳的转换，音画同步，异常值保护等等内容。因为较为琐碎，这里就不详谈了，感兴趣的读者可以直接阅读WebRTC的源码timing.cc和frame_buffer2.cc。
参考文献
[1] R. E. Kalman. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. Mar 1960, 82(1): 35-45 (11 pages)